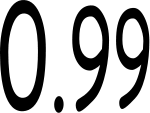 I've added a brand new section to the Mental Gym today!
I've added a brand new section to the Mental Gym today!
It's called Mental Division: Decimal Accuracy, and deals with converting division problems or fractions into their decimal equivalents as precisely as possible, without using a calculator.
The new tutorial starts by making sure you know how to divide by numbers from 2 through 11 by heart. Many fractions and division problems can be reduced to these problems, and become easier when you know the answers off the top of your head.
After that, I jump up to showing how to divide by several numbers near 100, including 100, 99, 98, 91, and 90. The answers are deceptively simple to work out.
Finally, the tutorial wraps up with showing how to cover a wider range of numbers, using just these strategies. For example, you'll learn how to handle dividing by 13 by turning it into division by 91. When you can't apply any existing division patterns, I even discuss estimating the decimal equivalent.
I wrote this tutorial because I've seen very few mental math tutorials that cover division with decimal accuracy, and those that do almost never cover numbers near 100.
Knowing how to convert a fraction to a decimal equivalent also works well with my recent tutorial on Estimating Square Roots. For example, let's say someone asks for the square root of 581.
Using the procedure taught in that article, you'd estimate that the square root of 581 is about 24 and 5/49ths. Using the new tutorial's conversion to decimal accuracy, you'd realize that 5/49ths is the same as 10/98ths, and so you can give the decimal equivalent of 24 and 5/49ths as 24.1020408163265306 and as much farther as you'd care to go!
The nice thing about the decimal accuracy addition to the feat estimating square roots is that you only have to use it when you can work it out. Even if you find you can't give an exact decimal, you simply leave them with an incredibly accurate fraction.
I'm open to adding more decimal conversion methods to this tutorial, so if you have any tricks for numbers not already covered there, let me know about them!